Christophe Olivier and Remy Croisille, of Finaltis, show how the Reverend Thomas Bayes can help deal with the pitfalls of putting Markowitz’s Modern Portfolio Theory into practice.
Modern Portfolio Theory as proposed by Harry Markowitz is mathematically crystal clear. However, putting theory into practice presents many pitfalls and often ends in disappointing results. One of the problems we face is estimating the parameters (returns, volatility and correlation) for the future, while only observations of the past are available. Practitioners resort to replacing the parameters by their estimators, which are in fact highly unpredictable.
Bayes’ theory allows for revising estimations of parameters based on observations and the probability laws of these observations.
The most visible consequence of the pitfalls of putting Markowitz’s Modern Portfolio Theory into practice is the extreme concentration of the resulting portfolios. In practice we tend to select a small number of stocks for which the recent observations of the parameters are better than the rest, which in no way guarantees that their real parameters are different or better than the others.
When the practitioner is confronted with the observed concentration problem, a quick remedy can be found by artificially increasing the diversification by adding constraints or factors such as:
• A maximum exposure per stock, per sector or per country;
• An arbitrary rule which decreases the weights of large positions in favour of smaller ones.
We have noticed that the result of such methods, which treat the symptoms rather than the cause, are driven by the constraints as opposed to the optimisation.
An alternative solution is to make additional hypotheses such as:
• All correlations are equal to zero and all the returns are equal, which leads to the risk parity approach;
• The returns are proportional to their volatilities, which leads to the maximum diversification approach.
Are such hypotheses coherent with the reality of our observations? This we do not believe to be the case, at least in the equity world.
YOUR MOST REVEREND…
So we propose a third solution using Bayes’ theorem.
Reverend Thomas Bayes (1702-1761) published just two papers in his lifetime; his work on conditional probability was published after his death by one of his friends and later validated by Laplace.
Bayes’ theorem states: P(A|B)=P(A) *P(B|A)/P(B) where, for two events A and B:
• P(A) is the probability that event A occurs.
• P(A|B) is the probability that event A occurs given that B has occurred.
By giving a formula to simply calculate conditional probabilities, Bayes’ theorem allows us to revise our estimation of a probability based on new information.
Monty Hall, the host of American TV gameshow Let’s Make a Deal, would ask his guest – hoping to win the prize, a flashy new car – to choose one of three closed doors; two of them hide a goat and a third the car.
The contestant starts by picking a door but doesn’t open it. The host, who knows where the car is, then opens another door, behind which there is always a goat. Then the host asks his guest if he would like to change door or stick to his original choice. What should the candidate do to optimise his/her chances of winning: switch or stick? There are generally two groups of respondents:
• Those who say that two doors remain, each having the same probability. So, it is pointless to change.
• Those who say that at the outset there was a one in three chance of winning and by sticking with the first choice, one still has a one in three chance. So, by changing, one must have a two in three chance; it is best to switch.
It is in fact a classic conditional probability problem, which is easy to solve with Bayes’ theorem. Let’s suppose, for this demonstration, that the contestant had chosen door number one and that the host had then opened door number three.
Of course, the host cannot choose door one because the contestant has chosen it. By opening a second door, which does not contain the car, we obtain new information.
By correctly taking this into account using conditional probability, we significantly improve our chances of winning from 1/3 to 2/3 by changing from door number one to door number two. By noting:
• P(C2) the probability that the car is behind door two ;
• P(D3) the probability that the host opens door three ;
• P(C2 | D3) the probability that the car is behind door two given that the host opened door three;
• P (D3 | C2) the probability that the host opens door three given that the car is behind door two.
Then Bayesians will assert:
• P(C2 | D3)= P (C2)* P (D3 | C2)/ P (D3)= (1/3) *(1/1) /(1/2) = 2/3
• P(D3 | C2)= 1/1: the host cannot open door one because the contestant chose it and he cannot open door two either because he knows the car is behind it : he has to choose door three!
• P(D3)= 1/2: the host cannot open door one because the contestant chose it, there are then two possible choices: door two or door three.
Bayes’ theorem is widely used in what is called Bayesian inference to revise estimations of a probability or a parameter based on observations and probability laws.
In our example of portfolio allocation, we proceeded by making a methodical analysis of the quarterly volatilities and correlations for all stocks across a period of 20 years.
In the case of volatility, for example, we observed, for each quarter, a volatility histogram showing between four to five humps corresponding to volatility levels where there were a large number of stocks. As such, we have modelled the universe of stocks as having just five possible levels of volatility.
Our research has illustrated the realised volatilities across the Euro Stoxx universe in December 2015. Although a histogram we produced did not seem to perfectly represent the theoretical line (calibrated), examination of the cumulative probability showed the model to be relevant.
The interpretation of collective information, that is to say the observation of realised volatilities, allows us to define volatility buckets with their associated probabilities.
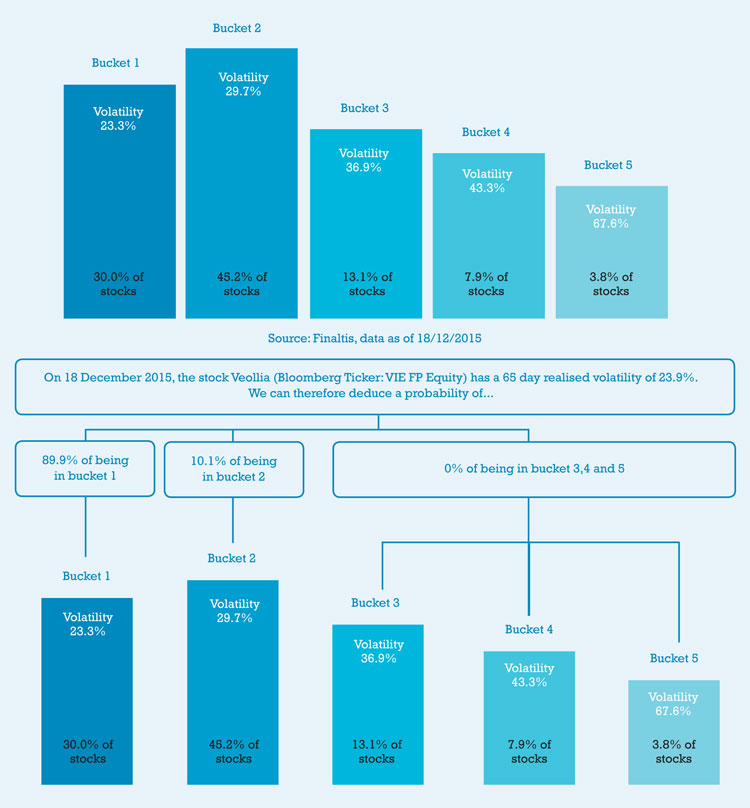
We find ourselves in the classic Bayesian inference framework where we can modify, based on our observations, the a priori probabilities of stocks belonging to each group or bucket.
If a stock were to have a realised volatility of 23.9%, which is close to the bucket 1 volatility, the probabilities would adjust as in the grapic on this page.
Our estimation takes into account not just the individual information of each stock but also collective information of our observations of all stocks and integrates, through a probabilistic calculation, the uncertain nature of the estimator.
Thanks, in part, to this revised estimator of volatility inspired by Bayesian probabilities, and a similar estimator of correlation, and a method inspired from Markov chains to model migration between buckets and an optimisation algorithm, this method is able, without adding artificial constraints, to generate optimal portfolios, which offer return/risk properties which are far superior to those of the benchmark index.
Thanks, Reverend Bayes!
Christophe Olivier is chief investment officer and Remy Croisille is head of research at Finaltis
©2016 funds europe





